Codes (first edition)
Here are all the code listings from the book, bundled together into a zipped directory. Alternatively, you can clone the git repo.
Below, you can browse through the same codes, chapter by chapter. These programs are discussed in detail in the main text so, to avoid duplication, they don’t contain comments.
Chapter 1: Idiomatic Python
| forelse.py | Illustration of the for-else idiom |
| plotex.py | Basic example of Matplotlib use |
| vectorfield.py | Visualizing a vector field via Matplotlib's streamplot() |
Chapter 2: Numbers
| kahansum.py | Compensated summation |
| naiveval.py | Naive evaluation of a mathematically tricky function |
| compexp.py | Computing the exponential function |
| recforw.py | Forward recursion |
| recback.py | Backward recursion |
| cancel.py | Example where rounding errors cancel |
| chargearray.py | Constructing an array of electrical charges |
| legendre.py | Evaluating Legendre polynomials and their derivatives |
| multipole.py | Multipole expansion for point charges |
Chapter 3: Derivatives
| finitediff.py | Finite-difference approximations to the first derivative |
| richardsondiff.py | Richardson extrapolation for finite differences |
| psis.py | Computing the wave function for two physical scenarios |
| kinetic.py | Evaluating the local kinetic energy |
Chapter 4: Matrices
| triang.py | Infrastructure for triangular matrices and testing |
| gauelim.py | Gaussian elimination |
| ludec.py | LU decomposition |
| gauelim_pivot.py | Gaussian elimination with partial pivoting |
| jacobi.py | Jacobi iterative method for linear systems |
| power.py | Power method for eigenvalue/eigenvector evaluation |
| invpowershift.py | Inverse-power method with shifting |
| qrdec.py | QR decomposition |
| qrmet.py | QR method for eigenvalues |
| eig.py | All eigenvalues and eigenvectors |
| kron.py | Kronecker product of two matrices |
| twospins.py | Two interacting spin-half particles |
| threespins.py | Three interacting spin-half particles |
Chapter 5: Roots
| fixedpoint.py | Fixed-point iteration |
| bisection.py | Bisection method |
| secant.py | Secant method |
| legroots.py | Zeros of Legendre polynomials using Newton's method |
| multi_newton.py | Newton's method for multidimensional problems |
| descent.py | Minimization via the gradient descent method |
| action.py | Discrete Newton method for extremizing the action |
Chapter 6: Approximation
| barycentric.py | Lagrange interpolation using the barycentric formula |
| splines.py | Cubic-spline interpolation |
| triginterp.py | Trigonometric interpolation using sines and cosines |
| fft.py | Fast Fourier transform |
| linefit.py | Least-squares straight-line fit |
| normalfit.py | Least-squares fitting using the normal equations |
| blackbody.py | Non-linear fitting for the Stefan-Boltzmann law |
Chapter 7: Integrals
| newtoncotes.py | Newton-Cotes quadrature |
| adaptive.py | Adaptive integration |
| romberg.py | Romberg integration |
| gauleg.py | Gauss-Legendre quadrature |
| montecarlo.py | Monte Carlo quadrature with importance sampling |
| eloc.py | Many-particle wave function and local energy |
| vmc.py | Variational Monte Carlo via the Metropolis algorithm |
Chapter 8: Differential Equations
| ivp_one.py | Initial-value problem solvers |
| ivp_two.py | Runge-Kutta for simultaneous differential equations |
| bvp_shoot.py | Boundary-value problem via the shooting method |
| bvp_matrix.py | Boundary-value problem via the matrix approach |
| evp_shoot.py | Mathieu equation via the shooting method |
| evp_matrix.py | Mathieu equation via the matrix approach |
| poisson.py | Poisson's equation in two dimensions via the FFT |
Errata (first edition)
- p. 124 For elimination (third bullet point) not to impact the determinant, this should refer (not to a linear combination, but) to “the sum of that row/equation with a multiple of any other row/equation”.
- p. 306 Problem 11 should say “Taylor expand
 and
and  “. Then, it should say “Plug these relations”.
“. Then, it should say “Plug these relations”.
- p. 363 “Observe that in
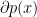 ” –> “Observe that in
” –> “Observe that in 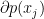 “
“
- p. 390 Problem 29 should be referring to polynomials with 2, 3, and 4 parameters (and “third degree” –> “three-parameter case” and “fourth-degree” –> “four-parameter case”)
- p. 436 In Eq. (7.120), there should be no product symbol
- p. 437 In Eq. (7.128), the sum should be over k
- p. 459 In fn 42, the integrand should be using x’
- p. 490 In problem 26, it would be more appropriate to say that
 can be given in terms of the first and second complete elliptic integrals
can be given in terms of the first and second complete elliptic integrals
- p. 491 In problem 31,
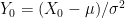 –>
–> 
- p. 491 In problem 34, you’re supposed to use Gauss-Legendre for “
 “
“
- p. 493 Problem 43: “the fact that
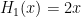 ” –> “the needed Hermite polynomials”
” –> “the needed Hermite polynomials”
- p. 556 Problem 25,
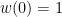 –>
–> 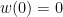
and
“. Then, it should say “Plug these relations”.
” –> “Observe that in
“
can be given in terms of the first and second complete elliptic integrals
–>
“
” –> “the needed Hermite polynomials”
–>